Acoustic signals: Basic principles

Overview
Sound fields and levels
Sound pressure level and the decibel scale

Overview

This page outlines some of the basic principles, terminology, and concepts that we use when talking about acoustic and audio signals. Many of the ideas (e.g., RMS levels, decibels, etc) translate easily to electrical and other types of signals, too.

Where relevant, we will introduce some terminology and concepts used in digital systems, including for digital audio – we often refer to this as a ‘discrete time’ system.

Sound fields and levels

A note on terminology

The terminology below is written largely in terms of sound pressure, $p$ . However, the core mathematical concepts apply equally well to sound intensity, particle velocity, volume velocity, voltages, currents, etc. We’ll use these concepts in many of the other pages here in the Resources section of this site.

Sound pressure

Sound can be specified in several ways. Of most relevance to microphones is the concept of sound pressure – i.e., the amount of force per unit area imparted by an acoustic wave (whether on the surrounding air or, ultimately, on a microphone diaphragm). We usually think of sound pressure as just the acoustic, i.e., varying, pressure above and below the ambient atmospheric pressure. Strictly speaking, we might specify

(1) $\begin{align*} p_{total} = p_{0} + p \end{align*}$

where $p_{total}$ is the total pressure at a point in space, made up from the static ambient atmospheric pressure $p_0$ , and the acoustic (varying) pressure $p$ .

In practice, we are nearly always interested in just $p$ , and fortunately many common microphones, especially omnidirectional designs, produce an output that only depends on $p$ , anyway. We implicitly assume the ‘0’ point of such signals to correspond to the static ambient atmospheric pressure, $p_0$ . The standard reference ambient atmospheric pressure $p_{0}$ is usually considered to be $10^5$ Pa (Pascals, aka. N/m $^2$ ). In typical audio-range scenarios, the magnitude of the acoustic pressure $p$ will be in the range of a few $\upmu$ Pa (micro-Pascals) to a few Pa (Pascals).

Root mean square (RMS) signal level (continuous time)

By their very nature, acoustic signals continuously vary in amplitude as time progresses. If we consider a very simple acoustic signal, such as a 1 kHz sinusoidal tone, we can identify several ways of describing its ‘level’. There is the peak positive level, the peak negative level, the ‘average’ level, and so on. However, often the most useful metric is the root mean square (RMS) level of the signal, evaluated over some window of time. For a signal $p(t)$ (sound pressure as a function of time) the RMS level is described in continuous time as the integral:

(2) $\begin{align*} p_{rms} = \sqrt \ \frac{1}{T} \int_{0}^{T} (p(t))^2 dt \ \end{align*}$

which describes a squaring of the signal at all times between 0 and $T$ , summing (integrating) the result, and taking the square root of this sum (integral).

Root mean square (RMS) signal level (discrete time)

In practical situations involving signals that have been sampled into a digital system (e.g., a digital audio recorder, or a computer), the discrete time version of the RMS calculation is more relevant and intuitive. The theory behind sampling of continuous time signals is extensive and fascinating, but this page will skip over most of the underlying technical details.

We consider that $p(t)$ is sampled at periodic instances in time, each separated by a time duration that we refer to as the sample period $T_s$ (where $T_s = 1/F_s$ with $F_s$ the system’s fixed sample rate), indexed by integer $n$ . We might call this sampled, discrete time signal $p[n]$ . The RMS level of this signal over a duration of N samples is then:

(3) $\begin{align*} p_{rms} = \sqrt \ \frac{1}{N} \sum_{0}^{N} (p[n])^2 \ . \end{align*}$

In many audio-range applications, i.e., where we care about acoustic signals in the audible range of approximately 20 – 20000 Hz, typical sample rates, $F_{s}$ , are 44100Hz and 48000 Hz. In some applications, such as where post-hoc pitch shifting of the recorded signals may be needed, higher sample rates may be used (for example, 96000 Hz or 192000 Hz).

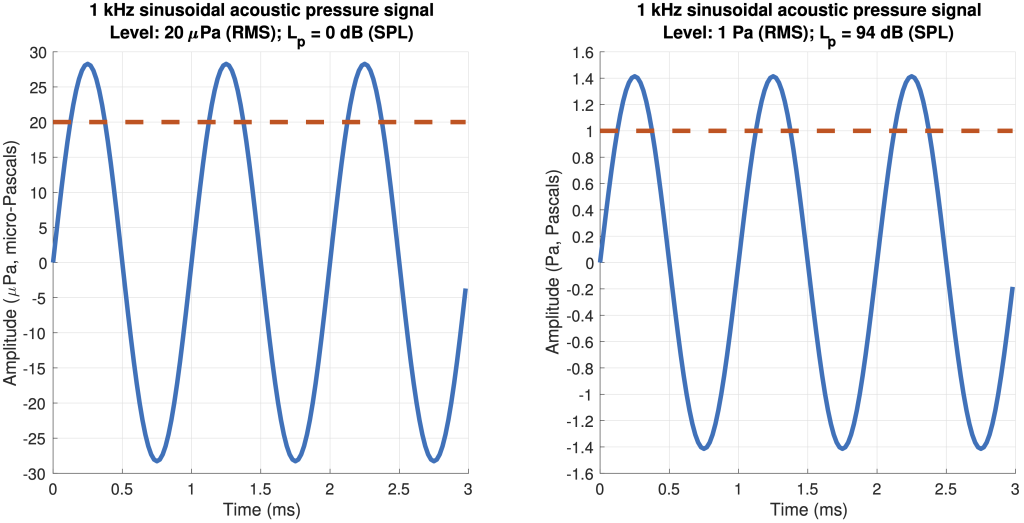
Relationship between a sinusoidal signal’s magnitude and its (RMS) level (both continuous and discrete time)

Where a signal is a pure sinusoid of constant frequency, some algebraic tweaking shows that there is a simple relationship between the magnitude of the signal and its RMS level. This is:

(4) $\begin{align*} p_{rms} = \frac{|p|}{\sqrt{2}} \end{align*}$

where $|p|$ is the magnitude of the signal $p$ (where magnitude can be thought of as the positive peak amplitude).

Sound pressure level and the decibel scale

In acoustics, the RMS sound level is used to define the so-called sound pressure level, $L_{p}$ , which we specify as the logarithmic ratio:

(5) $\begin{align*} L_{p} = 20 \log_{10} \left ( \frac{p_{rms}}{p_{ref}} \right) \end{align*}$

where $p_{ref}$ is a reference pressure, usually chosen as 20 $\upmu$ Pa (micro-Pascal) RMS. The sound pressure level for a sound pressure $p_{rms}$ measured as 20 $\upmu$ Pa is therefore:

(6) $\begin{align*} L_{p} = 20 \log_{10} \left ( \frac{20\cdot 10^{-6}}{20\cdot 10^{-6}} \right) = 20\log_{10}(1) = 0\ \mathrm{dB (SPL)}. \end{align*}$

The value of 20 $\upmu$ Pa is chosen because it corresponds, approximately, to the minimum sound pressure that is audible to humans in the mid-frequency range of $1-3$ kHz. In other words, an $L_{p}$ of 0 dB (SPL) corresponds to a sound that is ‘just’ audible for a human with healthy hearing, in the mid-frequency range. Most audible sounds therefore have a $L_{p}$ that is larger (more positive) than this. For example, an $L_{p}$ of 60 dB (SPL) would correspond approximately to normal spoken conversation in a reasonably quiet room.

Figure 1 illustrates how the magnitude and RMS level of a sound signal are related in the case of a pure tone sinusoidal signal at 1 kHz. The relevant sound pressure levels, $L_{p}$ , are also noted.

Contents